티스토리 뷰
퍼셉트론
다수의 신호를 입력으로 받아 하나의 신호를 출력하는 모델을 퍼셉트론이라고 하며 딥러닝의 기원이 되는 알고리즘이기 때문에 매우 중요하다.
퍼셉트론의 동작 원리를 보자!
y = 0 { w1x1+ w2x2 <= theata) or 1 { w1x1 + w2x2 > theta}
* 변수의 의미
이때 x1과 x2는 입력신호이며 w1와 w2는 가중치로 각각의 입력신호가 얼마나 중요한지를 결정해준다. theata는 얼마나
"쉽게" 1이 될 수 있냐를 결정지어준다.
단순한 논리 회로와 매개변수를 살펴보자!
두 신호가 입력신호로 주어지고 하나의 출력을 내는 퍼셉트론 모델을 살펴보자.
*AND게이트
=> 두 입력신호가 모두 1일때만 결과로 1이 출력되어야하고 이를 만족하는 w1, w2, theata는 무수히 많다.
=> (0.5,0.5,0.9)의 경우에 그 예가 될 수 있으며 두 입력신호가 모두 1일때만 1을 0.9를 넘어 출력결과가 1이 나오기 때문이다.
*NAND 게이트
=> 두 입력신호가 모두 1일때만 결과로 0이 출력되어야하고 이를 만족하는 w1,w2,theata에는 (-0.5, -0.5, -0.7)등이 있다.
*OR게이트
=> 두 입력신호가 모두 0일때만 결과로 0이 출력되어야하고 이를 만족하는 w1,w2,teatha에는 (0.3,0.5,0.2)등이 있다.
[핵심 포인트]
세가지 논리 게이트를 살펴보며 적절한 W1, W2, THEATA를 생각해보았나요? 퍼셉트론은 인간의 도움으로 매개변수 W1, W2, THEATA를 정합니다. 딥러닝이 퍼셉트론과 다른점은 매개변수를 직접 기계가 학습하며 최적의 매개변수를 만든다는 점에 있습니다.
=> 학습 : 기계가 스스로 최적의 매개변수를 찾아나가는 과정
퍼셉트론을 코드로 구현해보자!
우리는 THEATA를 이항해 편향 B를 만들 수 있으며 THEATA를 기준으로 1또는 0을 출력하게 되던 조건문이 0을 기준으로 1또는 0을 결정해 출력결과를 알아내도록 해봅시다.
* y = 0 { w1x1+ w2x2 + B <= 0) or 1 { w1x1 + w2x2 +B > 0}
*AND게이트
# 가중치와 편향의 개념을 도입한 AND게이트의 구현
#기본구현
import numpy as np
x = np.array([0,1])
w = np.array([0.5,0.5])
b = -0.7
print(w*x)
print(np.sum(w*x)+b)
AND게이트
def AND(x1,x2):
x = np.array([x1,x2])
y = np.array([0.5,0.5])
b = -0.7
tmp = np.sum(w*x)+b
if tmp<=0:
return 0
else:
return 1
print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))RESULT : [0. 0.5] -0.19999999999999996 0 0 0 1 ( 여러줄에 걸쳐서나옴)
*NANA와 OR
#NAND와 OR게이트의 구현
def NAND(x1,x2):
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
temp = np.sum(w*x)+b
if temp<=0:
return print("0")
else:
return print("1")
def OR(x1,x2):
x = np.array([x1,x2])
w = np.array([0.3,0.4])
b = -0.2
temp = np.sum(w*x) + b
if temp<=0:
return print("0")
else:
return print("1")
print("NAND")
NAND(0,0)
NAND(0,1)
NAND(1,0)
NAND(1,1)
print("OR")
OR(0,0)
OR(0,1)
OR(1,0)
OR(1,1)RESULT : NAND 1 1 1 0 OR 0 1 1 1 ( 여러줄에 걸쳐서나옴)
*위에서 봐오던 단층퍼셉트론(하나의 직선식)의 한계
*XOR게이트를 살펴보자
같은 입력값이 들어오면 0을 출력하고 다른 입력값이 들어오면 1을 출력해야하는 게이트이며 이를 만족하는 w1, w2, B가 있을까 생각해봅시다!
좌표평면을 통해 쉽게 생각해볼 수 있다.
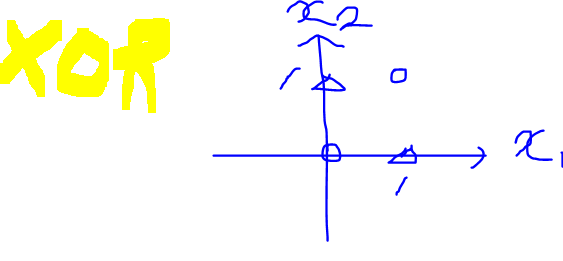
위의 그림을 통해 (0,0), (1,1)일때 출력의 결과가 0이 나와야하는 좌표를 동그라미로 찍었고, (1,0)과 (0,1)처럼 출력의 결과가 1이 나와야하는 좌표를 세모로 찍었다.
하나의 직선을 통해 영역을 동그라미 영역과 세모 영역으로 나눌 수 있을까?
=>불가능하다.
그렇다면 단 하나의 직선을 가지고 XOR을 표현할 수 없다면 퍼셉트론을 가지고 XOR을 표현할 수 없는 것일까?
=> 그건 아니다. 퍼셉트론을 가지고 XOR을 표현할 수는 있다. 다만 단층 퍼셉트론으로는 불가능하며 비선형을 표현하기 위해 여러 직선을 덧붙이며 다층 퍼셉트론을 활용해야한다.
다층 퍼셉트론을 통한 XOR게이트 구현!
=> x1과 x2가 NAND와 OR게이트를 지나 나온 결과 2개 s1, s2가 AND게이트에 들어가 y를 출력하면 다층 퍼셉트론을 이용해 XOR을 표현할 수 있다.
def NAND(x1,x2):
x = np.array([x1,x2])
w = np.array([-0.5,-0.5])
b = 0.7
temp = np.sum(w*x)+b
if temp<=0:
return 0
else:
return 1
def OR(x1,x2):
x = np.array([x1,x2])
w = np.array([0.3,0.4])
b = -0.2
temp = np.sum(w*x) + b
if temp<=0:
return 0
else:
return 1
def XOR(x1,x2):
s1 = NAND(x1, x2)
s2 = OR(x1,x2)
y = AND(s1,s2)
return y
print(XOR(0,0),XOR(0,1),XOR(1,0),XOR(1,1))RESULT : 0 1 1 0
[핵심포인트]
퍼셉트론의 층을 쌓으면 비선형적인 표현이 모두 가능하며 이론상 컴퓨터가 수행하는 처리를 모두 표현할 수 있다.
'데이터분석 및 인공지능 > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝-(5) MNIST 추론과정 (0) | 2021.09.25 |
|---|---|
| 밑바닥부터 시작하는 딥러닝-(4) 신경망 (0) | 2021.09.23 |
| 밑바닥부터 시작하는 딥러닝-(2) (0) | 2021.09.17 |
| 밑바닥부터 시작하는 딥러닝 -(1) (0) | 2021.09.17 |
- Total
- Today
- Yesterday
- 스택 파이썬
- 영화 리뷰 긍정 부정 분류
- 11053 백준
- 10866 백준
- CSMA/CD란?
- 코딩월드뉴스
- 백준 11053 파이썬
- 기사작성 대외활동
- stack 컨테이너
- 4963 섬의개수
- 효율적인방법찾기
- mm1queue
- 백트래킹(1)
- DRF 회원관리
- 백준 4963
- 소프트웨어공학설계
- c++덱
- 백준 15650 파이썬
- 백준 숫자놀이
- 온라인프로필 만들기
- 시뮬레이션 c
- 핀테크 트렌드
- 백준 10866
- 딥러닝입문
- 기본 텍스트 분류
- CREATE ASSERTION
- 모듈 사용법
- LAMBDA
- 파이썬 알아두면 유용
- 13886
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
